Hogyan keressünk féreglyukakat?
Fekete lyukakat manapság már "könnyű" találni, hiszen gravitációs hatásukon kívül egyéb jelekkel - például kifúvások, akkréciós korongok - is elárulják magukat. De hogyan ismerjük fel a féreglyukakat?
Bár a fekete lyukak létezésének lehetősége már Laplace munkáiban (Exposition du Systeme du Monde, II. 305 [1789]; Allgemeine geographische Ephemeriden, 603 [1799], magyar fordítása: Fizika 1978, 273. o.) is felmerült, néhány évtizeddel ezelőttig ezek az egzotikus objektumok csupán elméleti fizikusok szűk körének matematikai "játékszerei" voltak. Az észlelési és detektálási technikák rohamos fejlődésének köszönhetően azonban ma már általánosan elfogadott, hogy sok galaxis központjában több millió naptömegű fekete lyuk foglal helyet, illetve az, hogy bizonyos tömeghatár feletti csillagok fejlődésének végállomása is ilyen – igaz, az előbbinél nagyságrendekkel kisebb tömegű – objektum. A fekete lyukak a környezetükre gyakorolt gravitációs hatásuk, az általuk gerjeszett részecskesugárzások, anyagkifúvások (jetek), illetve a körülöttük lévő anyagbefogási korongok révén ismerhetők fel.

Féreglyuk, ahogyan a legtöbb (tudományos) fantasztikus filmben elképzelik.
[www.universetoday.com]
A féreglyukak a fekete lyukakhoz hasonlóan szintén az általános relativitás elméletéből következő matematikai (topológiai) objektumok, melyek a téridő két, esetenként egymástól távoli pontját kötik össze alagútszerűen. Az elképzelés Hermann Weyl német matematikustól, míg az elnevezés John Wheeler amerikai fizikustól származik, s azon az analógián alapszik, hogy egy féreg (kukac) is jelentősen lerövidítheti útját egy alma két pontja között, ha nem az alma felületén jut el A-ból B-be, hanem átrágja magát a gyümölcsön. A féreglyuk szájai közelében a téridő elkezd görbülni, a maximális görbületet a szájakat összekötő torokban éri el. A féreglyukaknak több fajtája képzelhető el. Összeköthetik ugyanannak az univerzumnak két pontját, de funkcionálhatnak két párhuzamos univerzum közötti "kapuként" is. Ez utóbbiakat gyakran Schwarzschild-féle féreglyukaknak vagy Einstein-Rosen hidaknak is hívják. Ha a féreglyuk átjárható (traversable), akkor a torkon keresztül anyag juthat át az egyik szájból a másikba. A legtöbb, az átjárhatóságot megengedő matematikai megoldás feltétele egy hipotetikus anyagforma (exotic matter) létezése is a torok közvetlen környezetében, amelynek negatív az energiasűrűsége.
A fekete lyukaktól eltérően a féreglyukak létezésére ma még nincs észlelési bizonyíték. Alexander Shatskiy, a moszkvai Lebegyev Fizikai Intézet munkatársa felvázolt egy elképzelést, hogyan lehetne ezen objektumok hatását megfigyelni, illetve hogyan lehetne megkülönböztetni őket a fekete lyukaktól.
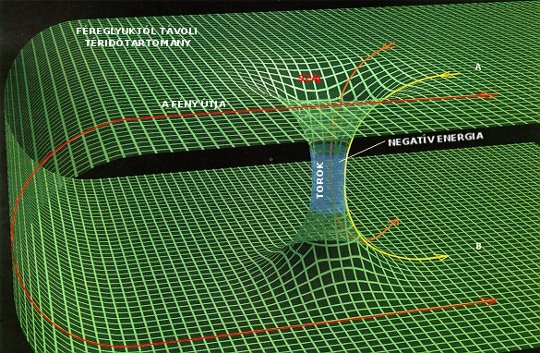
A féreglyukak a téridő két, egymástól egyébként távoli A és B pontját köthetik össze.
[www.universetoday.com nyomán]
A féreglyukak legjellemzőbb része az átjáró, a torok, melynek közelében a téridő görbülete nagyon nagy, eléri a hasonló tömegű fekete lyukak ún. eseményhorizontja körüli görbületét. Az eseményhorizont az a határ egy fekete lyuk körül, amelyen belüli események már nincsenek hatással a külvilágra. Az eseményhorizonton belülről indult fénysugár soha nem tud kijutni onnan, illetve az eseményhorizontot kívülről átlépő dolgok végleg elvesznek a külvilág számára. A fekete lyuk és a féreglyuk közötti legfontosabb különbség, hogy az utóbbinak nincs eseményhorizontja.
Ha anyagi részecskék át tudnak jutni a féreglyukon, akkor a fény, illetve bármely elektromágneses sugárzás is. Ezen alapul Shatskiy módszere, akinek vizsgálatai szerint egy egyenletes felületi intenzitást produkáló forrásból átjutott elektromágneses sugárzás intenzitásának a másik oldali száj körül jellegzetes szög szerinti eloszlása van. A szélén, a féreglyuk szájának megfelelő távolságnál nagy, a közepe felé egyre csökken az intenzitás, a centrumban, azaz a féreglyuk tengelyében pedig minimális, függetlenül a sugárzás hullámhosszától. Azaz a megfigyelő a féreglyuk körül egy fénygyűrűt láthatna, aminek külső széle éles, belső széle pedig fokozatosan halványul. A tengely irányában átláthatna a féreglyukon, s akár csillagokat figyelhetne meg az univerzum normál tartományaiból.
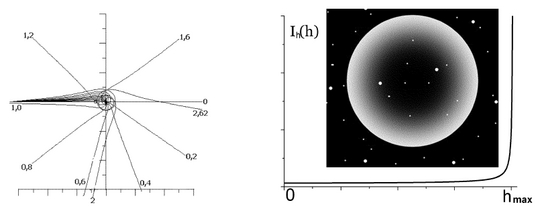
Féreglyukon átjutó fotonok szög, illetve a h ütközési paraméter szerinti eloszlása. Az ütközési paraméter a foton beesési irányának a féreglyuk tengelyétől mért távolsága.
[Alexander Shatskiy]
A féreglyukak által generált sugárzási gyűrűk megfigyelése ma még nem lehetséges, ehhez a maiaknál lényegesen jobb felbontású rádióinterferométerek kellenének, melyekkel részletesen lehet tanulmányozni olyan extrém területeket, például galaxismagokat, ahol elsősorban lehet számítani féreglyukak felbukkanására.
Természetesen nem szabad elfelejtkeznünk arról, hogy a féreglyukak létezésének elméleti lehetősége még nem jelenti azt, hogy valójában is léteznek. De ha léteznek is, valószínűleg nagyon instabil képződmények, így felhasználásuk bármilyen tér- vagy időbeli utazásra egyelőre a fikciók körébe sorolandó...
Lyukak a téridőben
Az Einstein-féle általános relativitáselméletnek számos, a józan ész számára meghökkentő következménye van. Közülük is talán a legbizarrabbak az úgynevezett féreglyukak: olyan „alagutak” a téridőben, amelyek kapcsolatot teremtenek két különálló világ vagy a mi világunk két távoli pontja között. Nemrég egy orosz elméleti fizikus olyan átjárható féreglyukak létezésének lehetőségéről számolt be, amelyek kellően stabilak és elég nagyok is ahhoz, hogy rajtuk keresztül akár intergalaktikus kapcsolatot létesítsünk...
A féreglyukak számos paradoxonra vezetnének (egyebek között lehetővé teszik az időutazást!), ezért a fizikusok nagy többsége az Einstein-féle téregyenletek olyan tisztán matematikai megoldásának tekinti őket, amely a valóságban nem létezhet. A kutatók egy kisebb, merészebb hányada ebből némileg engedve úgy véli, hogy kvantumos szinten, a vákuumfluktuációkhoz hasonlóan keletkezhetnek olyan „kvantumféreglyukak”, amelyek rendkívül rövid időre ugranak elő a „semmiből”, majd újra eltűnnek. Szergej V. Krasnyikov, a Szentpétervár melletti Pulkovói Obszervatórium elméleti fizikusa egy nemzetközi konferencián nemrég olyan eredményről számolt be, amely még ezen is túllép: makroszkopikus méretű, stabil féreglyukak létezésének lehetőségét vázolja fel. A kutató szerint „építeni” még nem tudnánk ilyeneket, ám kellő ügyességgel a nyomukra bukkanhatnánk a Világegyetemben.
Mindez túl fantasztikus ahhoz, hogy igaz legyen? Mielőtt egy legyintéssel félredobnánk, szellemi kalandnak sem utolsó, hogy közelebbről megismerkedjünk ezekkel a furcsa téridőalagutakkal és az átjárható féreglyukak nyújtotta lehetőségekkel.
Gidres-gödrös téridő
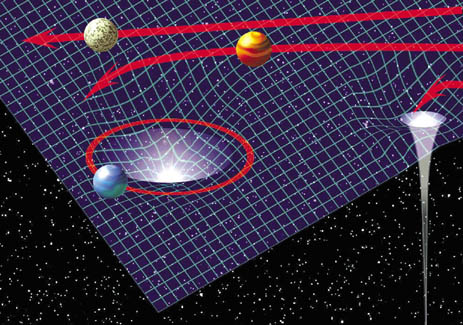
Az Einstein-féle általános relativitáselmélet szerint a téridő nem önmagában adott, az anyagtól függetlenül létező dolog, hanem szerkezetét a benne lévő anyag határozza meg. Az elmélet száműzi a tömegek közt ható gravitációs erőt, és a testek mozgását a tömegek (az anyag eloszlása) által meggörbített téridőben lehetséges szabad mozgásokkal írja le. Egy hagyományosnak tekinthető hasonlat a téridőt kifeszített gumilepedővel szemlélteti, amely a beléje helyezett tömegek alatt többé-kevésbé behorpad, a testek pedig az így kialakuló, gravitációs gödrökkel teli téridőben úgy mozognak, mint az elgurított golyók.
 |
|
1. ábra. A tömegek meggörbítik maguk körül a téridőt
|
Mivel négydimenziós – három tér- és egy idődimenziós – világunkat nem igazán tudjuk jól lerajzolni, az 1. ábrán egy beágyazási diagramot láthatunk: ez két térdimenzió elhagyása után visszamaradó kétdimenziós görbült felület három dimenzióba beágyazott képe, amely szemmel láthatólag éppen olyan, mint az említett gumilepedő egy részlete. Látható, hogy a tömegektől távol, ahol a téridő gyakorlatilag síknak tekinthető, a golyó egyenesen gurul (a), míg a tömegek közelében pályája elgörbül (b). Megfelelő sebesség esetén a golyó a gödör lejtőjén körbefutó körpályára is állhat (c) – így alakulnak ki például a Naprendszer stabil bolygópályái. Ha a golyó sebessége ehhez kevés, akkor bezuhan a gödörbe.
Az általános relativitáselméletben a tömegek téridőgörbítő hatását az Einstein-féle téregyenletek adják meg. Már 1916-ban, közvetlenül azután, hogy Einstein közzétette őket, Karl Schwarzschild német csillagász megtalálta a téregyenletek első, matematikailag szigorúan pontos megoldását egy gömbszimmetrikus, nem forgó test esetében. Csaknem másfél évtized múlva, amikor Einstein és Nathan Rosen nagyon gondosan megvizsgálta a Schwarzschild-megoldást, megrázó felfedezést tettek.
Eredményük megértéséhez nézzünk egy csillagot, amely már minden nukleáris tüzelőanyagát elfogyasztotta, s gravitációs összeomlásba kezdett. A kollapszus során a csillag körül a téridő egyre görbültebbé válik.
Fekete, fehér, igen, nem?
Ha az összeroskadó csillag tömege többszörösen meghaladja a Napét, akkor az összehúzódás addig folytatódik, míg a lyuk átmérője nullára nem zsugorodik, s az anyagsűrűség és vele a téridő görbülete végtelenre nő. A téridőben így kialakuló szingularitás az úgynevezett fekete lyuk, amely minden beléje kerülő anyagot végleg elnyel (még a fényt is). A fekete lyukhoz közeledő anyag akkor „tűnik el” a világból, amikor átlépi az úgynevezett eseményhorizontot: ez az a felület, amelyen belülről már lehetetetlen kapcsolatot teremteni a külvilággal. (Ez legfeljebb a fényénél nagyobb sebességgel volna lehetséges, az viszont – szintén a relativitáselmélet szerint – nem léphető át.) Gumilepedős hasonlatunkhoz (és az 1. ábrához) visszatérve mindez olyan, mintha a lepedő anyaga nem volna tökéletesen rugalmas, és a túl nagy terhelés hatására kilyukadna (d).
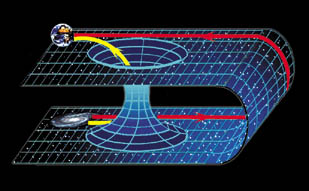
Az igazán megrázó felismerés azonban még hátravan. Matematikailag ugyanis a megoldás itt korántsem ér véget: a szingularitáson átlépve a tér görbülete újra csökkenni kezd, és az egyre öblösödő cső végül újra kinyílik. Ennél a nyílásnál azonban éppen a fordítottja történik mindannak, amit a fekete lyuknál láthattunk, mivel itt az anyag csakis kifelé áramlik: fehér lyuk jön létre, amelynek torkából állandóan anyag és energia lövell ki. Az így kialakuló bonyolult geometriájú szerkezet a 2. ábrán látható féreglyuk, más néven Einstein–Rosen-híd.
 |
|
2. ábra. A féreglyuk két különböző világot,
vagy ugyanazon világ
két távoli pontját kötheti össze
|
De mit kapcsol össze ez a híd? Matematikailag két lehetőség kínálkozik: két különálló világot vagy egyazon világ két távoleső tartományát. Számunkra talán az utóbbi még meghökkentőbb, mert így látszólag nincs akadálya annak, hogy egy ilyen féreglyukon át hipp-hopp, átcsússzunk a világ egyik pontjából egy távoli másikba. „Szerencsére” van egy bökkenő: ahhoz, hogy ezt megtegyük, keresztül kell haladnunk a szingularitáson, azaz a téridő végtelen görbületű és anyagsűrűségű tartományán, ami óhatatlanul végzetes következményekkel járna. (Tegyük hozzá, nem csak ez a baj. Gondosabb elemzéssel kimutatható: a szingularitás olyan természetű, hogy ezt az utat nemhogy egy űrhajós, hanem még egy klasszikus elemi részecske sem tehetné meg, ehhez ugyanis bizonyos szakaszokon a fényét meghaladó sebességgel kellene haladnia.)
De vajon létezik-e mindez a valóságban? Nos, a fekete lyukak létezését az eddig felhalmozott bizonyítékok tükrében ma már szinte senki sem vonja kétségbe, sőt, a legújabb röntgenműholdak tüzetesen vizsgálják a közvetlen környezetükben végbemenő folyamatokat. Fehér lyukak jelenlétére azonban egyelőre nincs semmiféle bizonyíték. (Igaz, ismeretesek olyan óriási energiafelszabadulással járó jelenségek – például a nagy energiájú gamma-kitörések –, amelyek bizonyos elképzelések szerint éppen a fehér lyukakkal magyarázhatók.)
Átjárható féreglyuk
A Schwarzschild-megoldás, mint említettük, a téridő geometriáját egy gömbszimmetrikus, nem forgó tömeg körül írja le. Ez idealizált eset, mivel a valóságos csillagok forognak, s (részben ezért is) nem tökéletesen gömbszimmetrikusak. Roy P. Kerr 1963-ban találta meg a téregyenleteknek azt a megoldását, amely figyelembe veszi a tömegek forgását is. A Kerr-megoldás téridőszerkezete már annyira bonyolult, hogy nem rajzolhatjuk ide, bár természetesen ennek is létezik a hozzáértők számára egyértelmű eligazodást nyújtó ábrázolása, az úgynevezett Penrose-diagram. Ez másfajta téridőtérkép, amely nagyjából úgy viszonyul az eddig bemutatott beágyazódiagramokhoz, mint a síkatlasz a földgömbhöz. A Penrose-diagramon nyomon követhető a forgó fekete lyuk eseményhorizontján belülre zuhanó űrhajós további sorsa.
Kip Thorne 1985-ben olyan megoldást talált, amelyben megkerülhető a szingularitás, s az utazót nem éri utol baljós végzete. Érdekességként idekívánkozik, hogy a kutató barátjának és professzortársának, Carl Sagannak a kérésére látott a munkához, akinek Kapcsolat című művében a hősnőnek (a megfilmesített változatban Jodie Foster játszotta) igen rövid idő alatt kell eljutnia a Földről a Vega csillag rendszerébe.
A Thorne által talált átjárható féreglyuknak „csupán” egyetlen szépséghibája volt: ahhoz, hogy a bejáratai stabilan nyitva maradjanak, a belsejében negatív energiasűrűségű anyagnak kellett lennie, amely negatív téridőgörbületet hoz létre, s például a fényt nem maga felé, hanem éppen az ellenkező irányba görbíti. Ilyen egzotikus anyag egyelőre nem ismeretes, bár az elektromágneses tér vákuumfluktuációiban átmenetileg néha kialakul efféle állapot.
 |
|
3. ábra. A kvantumhab
|
Kérdés, hogy ha felfedeznénk és netán elő is állítanánk ilyen egzotikus anyagot, akkor építhetnénk-e átjárható féreglyukat. Megoldást a kvantumfizika ígér. Alkalmasan kis léptékben ugyanis a Világegyetemben is érvényesül a Heisenberg-féle határozatlansági reláció. Kvantumszinten ezért a vákuumot úgynevezett kvantumhab tölti ki (3. ábra), amelyben a határozatlansági reláció által megszabott rövid időre fekete-fehér lyukpárok és féreglyukak ugorhatnak elő a semmiből, majd tűnhetnek el, ahhoz hasonlóan, ahogy az elektromágneses vákuumban a fotonok és az elektron-pozitron párok teszik. Feltéve, hogy egy ilyen előugró féreglyuk torkába valami módon egzotikus anyagot tudnánk tömni, stabilizálhatnánk, majd egyre nagyobbra pumpálhatnánk.Krasnyikov eredménye éppen ezen a ponton kapcsolódik a történethez. A féreglyuk fenntartásához és felpumpáláshoz szükséges egzotikus anyagot ugyanis a kutató számításai szerint maga a féreglyuk is létrehozhatja, pontosabban a körülötte kialakuló, negatív görbületű téridőszerkezet vákuumfluktuációi termelhetik egy önmagát erősítő folyamatban. Eszerint tehát van lehetőség átjárható féreglyuk kialakulására.
Az időgép
Ha viszont létezhet elég nagy méretű, átjárható féreglyuk, akkor az Thorne szerint időgépként működhet. Gondolatkísérlete nyomán képzeljük el, hogy a féreglyuk egyik szája a professzor nappalijában, a má-
sik pedig a kertben álló űrhajóban van, amellyel felesége, Carolee kisebb űrutazásra indul. Az űrhajót relativisztikus sebességre gyorsítja, majd egynapnyi utazás után visszafordul, s újabb egy nap elteltével házuk kertjében landol. A professzor a kettőjüket összekötő féreglyukon átnézve azonnal látja ezt, és a kertbe siet, hogy üdvözölje nejét. Igen ám, de az űrhajót nem találja ott! Caro-
lee órája ugyanis az űrhajóban a relativisztikus sebesség miatt sokkal lassúbb ütemben jár, s a nála eltelt 2 nap a professzor órája szerint 5 év. Thorne tehát csak 5 év múlva találja a kertben az űrhajót és feleségét (aki eközben mit sem, vagyis mindössze 2 napot öregedett). Az utazás kezdetétől a befejezésig a lyuk egyik szájánál 2 nap, a másiknál 5 év telt el, miközben a lyukon keresztül bármikor átbújhatnak egymáshoz, azaz öt éven belül tetszőlegesen „ugrálhatnak” az időben! Hogy ez kész őrület? Igen, egyike azoknak a képtelen időparadoxonoknak, amelyeket nagyon jól ismerünk a tudományos-fantasztikus irodalomból.
Amikor Thorne látta, hogy az átjárható féreglyuk elvben megteremtené az időutazás lehetőségét, azonnal keresni kezdte, milyen fizikai törvény léphetne közbe, amely megakadályozná az időgép működtetését. Olyan mechanizmust keresett, amely szétrombolja a féreglyukat, még mielőtt az működésbe lépne. Az eredmény azonban meglehetősen sovány volt, s csupán azt a lehetőséget hagyta, hogy bizonyos kvantumgravitációs vákuumfluktuációk annyira fölerősödhetnek, hogy lerombolják a féreglyukat. A kvantumgravitáció elmélete viszont egyelőre annyira kidolgozatlan, hogy az erre alapozott érvelés nem túl meggyőző.
A kronológiavédelmi elv
Mindebből úgy tűnik, a fizika törvényei lehetővé teszik olyan féreglyuk kialakulását, amelyen „keresztül” időgépet működtethetünk. Annyit azért vegyünk észre, hogy ez az időgép, legalábbis az egyik irányban, csak korlátozott utazást tesz lehetővé: az időgép megalkotása előtti időkbe még így sem juthatnánk vissza. Így az a paradoxon, hogy az időben visszaugorva az időgép feltalálója megöli önmagát, még mielőtt a gépet feltalálná, itt nem alakul ki. Írott történelmünket tehát – legalábbis „az első időgép előtti korokra” – nem kell átírni. Ez azonban legfeljebb a történészek számára lehet megnyugtató...
A fizikus, ha végképp nem tud megbirkózni egy ellentmondással, előbb-utóbb felállít egy olyan általános elvet, amely lehetetlenné teszi az ellentmondás megvalósulását. Jó példa erre a termodinamika második főtétele, amely egyik megfogalmazásában a másodfajú örökmozgó (perpetuum mobile) megépíthetetlenségét mondja ki. (Ez, persze, nem akadályozza meg a lelkes feltalálókat abban, hogy újabb és újabb örökmozgók ötletével álljanak elő.) Vajon nem lehetne ennek mintájára azt is kimondani, hogy márpedig időgép nem építhető? Ez az axióma egy csapásra megoldaná a problémát, ráadásul olyan általános rendezőelvvé válhatna, amely segítene kirostálni a másképp ki nem zárható, de ellentmondásra, paradoxonra vezető lehetőségeket. Itt nem csupán az időutazásra kell gondolnunk, hanem számos, még kiforratlan részecskefizikai és kozmológiai modellre, nem is szólva a kvantumgravitáció elméletének teljesen ingoványos területéről.
Kimondható ilyen elv. Nem létezhetne a természettudomány (sőt ember sem!), s teljes káoszba fulladna a világ, ha nem érvényesülne benne az okság elve. Minden eddigi tapasztalat arra mutat (és ezt bizonyos számítások is alátámasztják), hogy a Világegyetemben működik egy általános érvényű törvényszerűség, az úgynevezett kronológiavédelmi elv. Ez, miként a neve is mutatja, sosem engedi felborulni a dolgok ok-okozati sorrendjét. Ha valakit netán a tudomány minden eddig felgyülemlett tapasztalata sem győz meg erről, akkor már csupán Stephen Hawkingnak, korunk legnagyobb élő kozmológusának szellemes érvelésére hivatkozhatunk. Szerinte ugyanis mi sem bizonyítja jobban ennek az elvnek az érvényesülését, mint az a tény, hogy eddig még nem özönlött el bennünket a jövőből érkező turisták hada...
|

