Ezt a részt rögtön azzal kezdeném, hogy szerintem az idő mint fizikai realitás nem létezik. A természetben vannak folyamatok, a folyamatok pedig események láncolatából épülnek fel. Az események láncolatát pedig ok-okozati viszonyok alakítják ki. Mi emberek ezt a láncolatot az idő teléseként fogjuk fel és hajlamosak vagyunk azt hinni, hogy az idő éppen olyan konkrét fizikai dolog mint pl. az anyag. Szerintem az anyagi folyamatok valóban zajlanak, az idő pedig csak a mi felfogásunkban létezik. Az einsteini relativitás elmélet szerint az időt tetemesen megnyúltnak mérhetjük a saját időnkhöz viszonyítva a hozzánk képest gyorsan mozgó rendszerben. Az idő megnyúlása azt a gondolatot keltheti bennünk, hogy az időnek fizikai jellemzői vannak. De az idő megnyúlása csak egyfajta viszonyítási dolog, az egymáshoz képest mozgó rendszerek sebesség-viszonyaiból adódik. Természetesen számolunk az idővel, a legtöbb fizikai képletben szerepel. Ez rendben is van, mert egyfajta mércét ad a folyamatok leírására. De úgy gondolom, hogy nem lehet azt mondani, hogy itt van az idő a maga fizikai valóságában. Hogy az időt mérni is lehet szintén félreértésre vezethet, mert akkor is csak fizikai folyamatokról van szó, amelyeknek az ismétlődő szakaszait használjuk fel a mérésre.

Az idő fenti értelmezése szerint az időszakaszok a végtelenségig oszthatók, hiszen az idő csak a mi felfogásunk szerint létezik. De ha azt is figyelembe vesszük, hogy idő-fogalmunk az események láncolatát tükrözi, akkor azt kell megvizsgálnunk, hogy vajon van-e olyan szituáció amelynél ez a láncolat már nem értelmezhető világosan. Ez a helyzet pedig az ősrobbanást követő 10^(-43)másodpercen belül volt, ezt nevezik a Planck-időnek. Ezen időtartamon belül a tér mérete 10^(-33)cm (Planck-távolság) volt. Az Univerzum ezen fázisában a Heisenberg-féle határozatlanság volt a mértékadó törvény, ahol a tér és az idő teljesen egymásba mosódott. Ebben az esetben nem lehet beszélni eseményekről, folyamatokról. Ezért a világunkban megszokott idővel csak a robbanást követő 10^(-43)s eltelte után számolhatunk. Ez a pont volt a valós idő kezdete. Egyébként jelen világunkban sem értelmezhető az idő a Planck-távolságon belüli tértartományban. Bár elvileg az idő a végtelenségig osztható, a valóság azonban egy pont után gátat szab az idő további oszthatóságának. Tekinthetjük úgy is, hogy az idő kvantuma a 10^(-43)s.

Hogyan lehet akkor mégis leírni az időt? Önmagában sehogy sem, de ha a fizikai folyamatok szempontjából közelítjük meg a dolgot, akkor már mondhatunk róla valamit. A legjobb ha e célból a periodikus változásokat vesszük alapul. A rezgések szinte mindenütt jelen vannak. Ha csak arra gondolunk, hogy az elemi részecskéknek hullám természetük is van, akkor már a rezgéseknél vagyunk, mert hullám nincs rezgés nélkül. Miből adódik ez a hullámtermészet? Ha a húrok olyan szerkezetére gondolunk mintha rugók lennének, akkor ezek kilazulva rezeghetnek is, sőt át is adhatják egymásnak a rezgéseket, ami a hullámok kialakulását jelenti. Az elemi részecskék húrok sokaságából tevődnek össze. A részecskét felépítő húrok rezgései összegződnek és felharmónikust hoznak létre. Egy ilyen részecske azon túl, hogy a húrok csomóba kapcsolódása révén jött létre (ez képviseli a részecske-jelleget) egyfajta rezgésállapottal (saját-rezgés) is jellemezhető (ennek terjedéséből adódik a hullám-jelleg). Egy atomból kiinduló hullám nem áll meg az atom határánál, hanem azt a szabad húrok is továbbítják valameddig. Ezért van az, hogy egy atomi részecskét leíró hullámfüggvény túlnyúlik az atomon és nem lehet pontosan meghatározni egy atomnak a peremét. A szabad húrok, melyek a teret feszítik ki, már jobban kilazult rugókhoz hasonlóak. Saját rezgésük csekélyebb, de más részecskék által gerjesztett rezgéseket továbbítják. A rezgések folyamatának (a sorrendiség és együtt-történés) leírásához bevezetjük az időt. A mindennapi gyakorlatban inkább a mi emberi léptékünkhöz közelebb álló folyamatokat szoktuk használni az idő mérésére, mint a Föld keringését a Nap körül. Ezt aztán oszthatjuk kisebb részekre vagy képezhetünk nagyobb időtartamokat is. A pontosabb mérés atomórával történik, amelynél egy kitüntetett atom fentebb említett saját-rezgését használják etalonként.

Az egymáshoz képest bizonyos sebességgel mozgó rendszerek idő-dilatációját a következőképpen kell érteni. Ha egy rendszer sebességét a fény sebességéhez viszonyítjuk, akkor ezt a viszonyt a v/c aránnyal tudjuk kifejezni, ahol v a rendszer sebessége, c pedig a fénysebesség. Mivel a c egy konstans érték, ezért az bármilyen sebességgel mozgó rendszerből mérve ugyanannyi. A fenti arány figyelembe vételével egy un. Lorentz-transzformációt alkalmazva kiszámítható, hogy egy kisebb v1/c arányú sebességgel mozgó rendszerből nézve egy nagyobb v2/c arányú sebességgel mozgó rendszer által megtett úthoz szükséges idő rövidebbnek adódik, mintha azt a v2 sebességgel mozgó rendszerben mérnénk. Azaz a nagyobb sebességgel mozgó rendszer ideje megnyúltabbnak látszik a kisebb sebességgel mozgó rendszerből nézve. Ha az egyik rendszer sebessége a másikhoz képest megközelíti a fény sebességét, akkor az időnek ez a relatív megnyúlása már tetemes lehet. A gyorsabban mozgó rendszerben lévő nem érzékeli az idő-intervallumok megnyúlását, hiszen a saját idője szerint minden a legnagyobb rendben megy, ő az eltelt életéveit ugyanannyinak méri, mint a másik rendszerben élő vele egykorú társa a saját idője szerint. De a kisebb sebességű rendszerben élő számára úgy tűnik, hogy a másik órája lassabban jár, azaz egy adott pillanatban ő kevesebbnek méri a másik életkorát, azaz a másik fiatalabbnak tűnik számára őhozzá képest.

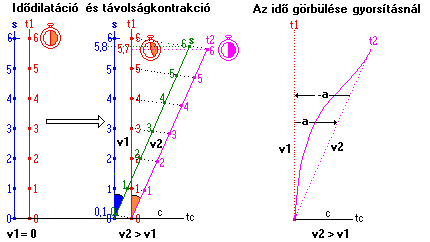
Az ábra első része két rendszert mutat, az egyiket állónak tekintve (v1=0) a másik ehhez képest v2 sebességgel mozog. Mindkét rendszerben a 6 egységnyi s út megtételéhez 6 egységnyi időre van szükség. A saját idője szerint mindkét rendszerben lévő így is méri a megtételhez szükséges időt. De a v1 sebességű rendszerből nézve (a v1 sajátidője szerint mérve) a v2 rendszerbeli rövidebb idő alatt teszi meg az utat (5,7 időegység). Egyben a megtett út is rövidebbnek látszik. Azaz a v1 rendszerből nézve a v2 ideje megnyúltnak (hosszabb időegység), a hosszúság pedig rövidebbnek tűnik. Ha a v2 fénysebességgel(c) mozogna v1-hez képest, akkor az idő megnyúlása végtelen nagynak látszana, a hosszúság pedig végtelen kicsinek. Az ábra szerint ez az eset akkor állna elő, amikor a bezárt szög 90 fokos lenne. Az ábra a v1 rendszer szemszögéből mutatja a látszólagos idő-dilatációt, de a v2 rendszerből nézve a v1 rendszer órája késne, hiszen relatív sebességekről van szó. A valóságban ez az egész nem ilyen lineáris, de a dolog lényegének megértése képletek nélkül talán így is elérhető. Az ábra második része azt szemlélteti, hogy a gyorsítás ill. lassítás alkalmával az idő egy görbét ír le amíg az egyik rendszer egy másik rendszer sebesség állapotát eléri. Nagy tömeghez közeledve szintén lelassul az idő ill. attól távolodva újra gyorsabbá válik, hiszen a gravitáció és a gyorsulás a relativitás elmélete szerint megkülönböztethetetlen ebből a szempontból. Egy erős gravitációs térben lévő óra szintén lassabban jár mint egy gyengébb gravitációs térben lévő óra.

A speciális relativitás elmélete
Az egésznek a lényege az, hogy a fény sebessége vákuumban egy konstans érték (~300000 km/s) függetlenül attól, hogy milyen rendszerben (álló vagy mozgó) terjed. Minden más sebesség ettől csak kisebb lehet, és az egyes mozgó rendszerek (itt inercia-rendszerekről van szó) sebességét a fény sebességéhez viszonyítjuk, akkor alkalmaznunk kell a Lorentz-transzformációt az idő, a távolság és a tömeg esetében. Ha egy rendszer v sebességgel mozog (egyenes vonalú egyenletes mozgást végez), akkor a rendszerhez tartozó idő megnyúlik, a mozgás irányába eső hosszúságok megrövidülnek, a tehetetlen tömeg pedig megnő a v/c függvényében egy állónak tekintett rendszer hasonló fizikai mennyiségeihez mérten, és a különböző sebességgel mozgó rendszerek sebességét sem lehet algebrai módon összegezni. Mindez azt jelenti, hogy nem lehet egy "világ-órát" használni, vagy nem lehet ugyanazon méter rúd szerint értelmezni a távolságokat a világ bármely pontján. Az egyik rendszerben egyidejűnek számító események egy másik rendszerből nézve különböző időpontokban történhetnek, ill. az egyik rendszerben egy adott helyen történő események a másik rendszerből különböző helyeken látszhatnak. A tér és idő tehát szorosan kapcsolódik egymáshoz.

Az általános relativitás elmélete
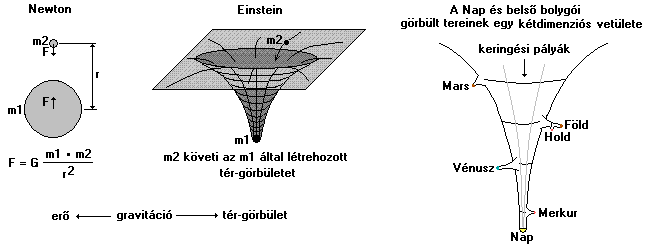
Ez már tágabb értelemben szemléli a fenti jelenségeket, hiszen szigorúan véve egyenes vonalú egyenletesen mozgó rendszerek (vagy nyugalomban lévő rendszerek) - azaz inercia-rendszerek - nem is fordulnak elő az univerzumban. Minden kering vagy forog vagy valamilyen pályát ír le, ami eltér az egyenestől. Mindezért a gravitáció a felelős. Azaz ebben az elméletben már a tér és idő mellé az anyagot is figyelembe kell venni. Az elmélet kimondja, hogy a világ bármely pontjában lévő anyagra a világ összes anyagának gravitációja hat, azaz a térben pontról-pontra változik a gravitációs hatás. Ráadásul a gravitációs hatás is másképp számolandó az egymáshoz képest mozgó rendszerekből, hiszen a tömegre is érvényes a Lorentz-transzformáció. Mindez azt jelenti, hogy a tér bármely pontjához más és más idő-intervallumok és hosszmértékek tartoznak. A pontról-pontra változás miatt pedig nem lehet euklídészi térben számolni, hanem görbült teret kell alkalmazni. Ennek az elméletnek a matematikai leírása már nyílván bonyolultabb mint a speciális relativitás elméleté, amely csak a tér-idő kapcsolatát vizsgálja, elvonatkoztatva a gravitációtól, addig az általános relativitás elmélet az anyag-tér-idő összefüggésben vizsgálja a jelenségeket, éppen a gravitáció egy a korábbitól eltérő értelmezését vezetve be (erő helyett térgörbület).
A newtoni ill. az einsteini garavitációs elmélet tehát alapelveiben különbözik egymástól. Newton a gravitációt erőtérként kezelte, amíg Einstein a tér görbületeként azonosította. A newtoni elmélet csak bizonyos korlátok között igaz, hiszen könnyen belátható, hogy a nevezőben szereplő távolság-négyzet miatt a zérushoz közelítő távolságok esetén a gravitációs erő a végtelenhez tart, ami nyílvánvalóan lehetetlen hiszen a gravitációs erő olyan nagy gyorsulást jelentene, ami miatt egy test túllépné a fénysebességet. Tehát csak nagyobb távolságok esetén használható a képlet. Egyéb hibái is vannak pl. nem tartalmazza az időt és a túl nagy gravitáció esetén sem használható. De bizonyos határok között jól működik. Még ma is számolnak vele a csillagászok.
Az einsteini elmélet már kiküszöböli a fenti problémákat, viszont ez sem teljes, mert csak a makroszkópikus világra érvényes, nem veszi figyelembe a kvantumfizika törvényeit. Einstein ugyan már ismerte ezeket a törvényeket, de ezek annyira újak és meghökkentőek voltak még, hogy nem tudta elfogadni a kvantumfizika furcsaságait ("Isten nem kockázik"). A szingularitást az ő elmélete sem tudja leírni.

Megjegyzés:
A tudományos világ Einstein neve alatt jegyzi a relativitáselméletet, de azt meg kell említeni, hogy a ennek előzményei voltak: Maxwell mondta ki a fénysebesség konstans voltát, Lorentz és mások már levezették a transzformációs egyenleteket és még mások - főként matematikusok - működtek közre a görbült tér (Riemann-féle) fizikai alkalmazásának adaptálásában, sőt még a híres tömeg-energia összefüggést is megfogalmazták már korábban. Einstein felesége (Mileva) is tevékenyen részt vett az elmélet megalkotásában.

Newton az időt egy nyílvesszőhöz hasonlította, egyenes, egy irányba mutat, ütemét nem változtatja. Ez volt az abszolút idő fogalma. De már Einstein előtt is rájöttek, hogy ez nem így van, az idő nem egy állandó valami mert az egymáshoz képest mozgó rendszerek esetében nem mindegy, hogy melyik rendszerből mérjük az időt. Ezért Einstein az időt inkább egy folyóhoz hasonlította, amelynek folyása le is lassulhat egy széles mederben, de fel is gyorsulhat amennyiben a medre leszűkül. Sőt görbült is lehet akárcsak a folyó kanyarulata. A mai felfogás szerint ezt a hasonlatot annyiban módosították, hogy az idő folyama akár teljes hurkot is leírhat, sőt el is ágazhat. Leírhat egy olyan kanyart, amelynél az idő egy múltbeli állapotához ér vissza. Ez felveti az időutazás lehetőségét. Az elágazáson azt kell érteni, hogy az idő két különböző kvantumtérben folyik tovább, azaz egy másik Univerzum is keletkezik az elágazáskor. Az időnek ezzel az elágaztatásával lehet feloldani az időutazásból eredő paradoxonokat, pl. olyanokat mint amelynél valaki visszamenve a múltba találkozik saját ifjúkori énjével, akit megöl. De akkor hogyan érhette meg a jelenkori korát? Az ilyen logikai bukfenc úgy oldható fel, hogy az idő kettéhasad, két kvantumtér keletkezik, az egyik amelyik a jelenlegi életnek megfelelő, a másik a halott énnel együtt már egy újabb világot jelent. Mindez azt is jelenti, hogy nem lehet csakúgy eltűnni az egyik világból és átlépni egy másikba, vagyis nem lehet megkettőzni magunkat egy időutazással és két időpontban is létezni, miközben mi ugyanazok maradunk. Halálunk bekövetkeztével sem tűnünk el a világból, testünk egy darabig még egyben marad, majd fokozatosan szétoszlik, de a testünket felépítő atomok - szétszóródva ugyan - még nagyon sokáig megmaradnak, és testünk atomjainak jelentős része új életek felépítésében vesz részt. A lélekkel kapcsolatos kérdések boncolgatása pedig nem a fizika feladatköre mert a fizika csak az anyagi világ törvényeinek megismerését tűzte ki célként. Felvetődhet a negatív idő gondolata is annak kapcsán amikor az esetleg zárt Univerzum a tágulás után visszafordul összehúzódásba. Ilyenkor a dolgok gyakorlatilag fordítva történnének, mint a táguláskor, hasonlóan ahhoz mint amikor egy filmet hátrafele játszanak le. Ez azt a gondolatot szülheti, hogy az idő negatívvá válva visszafele pörög. Az Univerzumot kívülről nézve valóban ez lenne a látszat. Valójában mégsem így van. Az események láncolata nem fordulna meg, vagy más megközelítésben az ok-okozati viszonyok továbbra is fennmaradnának. Az idő tehát ugyanúgy előre pörögne, miközben a galaxisok egyre közelednének egymáshoz egészen az egy pontba való összeomlásig. De addig amíg még egyáltalán lehetséges lenne az élet a csillagászok még sokáig a vöröseltolódást mérnék a kékeltolódás helyett, mert még mindig az összezuhanás előtti korszak felől érkező fényt látnák. Ha történetesen éppen már meg is történt volna a visszafordulás zsugorodássá, észre sem vennénk, az élet ugyanúgy zajlana tovább. Több milliárd év után az élet nyílván megszűnne a megemelkedett hőmérséklet, az erős sugárzások és az ütközésekből eredő kataklizmák miatt.

A fentiek értelmében mondhatjuk, hogy az idő sem abszolút. Ez azt jelenti, hogy az időt is tekinthetjük görbültnek akárcsak a teret. És ezzel el is érkeztünk az egységes téridő szemlélethez.