Történet

Az elõzõ fejezetben, amikor anyagról és erõkrõl beszéltünk, valójában tömegrõl és gravitációról is beszéltünk. A gravitációt, mint a világegyetemet átható általános erõt a természettudósok a 16-17. század során ismerték fel, a Naprendszer és a Föld tanulmányozása során. Ekkoriban vált elfogadottá Kopernikusz De Revolutionibus... címû mûve nyomán, hogy a Föld a többi bolygóval együtt mozog a Nap körül, azaz nem a Föld a világmindenség központja. Késõbb Kepler írta le a bolygók három mozgástörvényét:

• A bolygók pályája ellipszis alakú, melyek egyik gyújtópontjában helyezkedik el a Nap. A kör és elliptikus alakú pályák fókusza és periódusa azonos.
• A sugárvektorok azonos idõ alatt azonos területet súrolnak, azaz a keringési sebesség a Nap-Föld távolság függvényében változik.
• A különbözõ bolygók periódusidejének négyzetei úgy aránylanak egymáshoz, mint a Naptól mért átlagos távolságuk köbei.

Galilei mondta ki a tehetetlenség elvét - azaz minden test megtartja egyenes vonalú egyenletes mozgását, ha erõ nem hat rá. Newton ismerte fel, hogy az egyenes vonalú egyenletes mozgás helyett az égitestek kúpszelet-pályái akkor jöhetnek létre, ha a görbe (egyik) fókuszában van a változtatást okozó erõ. A Föld esetében a vonzóerõ sugárirányú, azaz a Nap irányába hat. Newton tette általánossá az ebbõl a megfigyelésbõl leszûrhetõ következtetést az egyetemes tömegvonzás elméletével, s a gravitáció egyetemes érvényének felismerésével. Newton felfogása szerint a gravitáció hatása pillanatszerû, azaz mozgó tömeg új helyzetében azonnal új erõ észlelhetõ. Newton megfigyelései mindaddig az egyetlen magyarázatot adták a világegyetem mozgására, amíg az atomi világ és az igen nagy sebességek és távolságok tanulmányozásáig el nem jutott a fizika és a csillagászat. Einstein módosította Newton elképzeléseit, és kimondta azt hogy semmi sem haladhat gyorsabban a fény sebességénél. A korábban különállónak vélt tér és abszolút idõ egy rendszert, téridõt alkot. A gravitáció terjedése is részben hullámtermészetû, és a fenti sebességi korlátnak úgy engedelmeskedik, hogy meggörbíti a téridõt. Einstein relativitás elmélete szerint mindennek aminek energiája van, tömege is van, s a gravitáció hat rá, így az energiával rendelkezõ fényre is.

Földi viszonyok és földtani objektumok esetében a sebességek és tömegek olyan kicsik, hogy az Einstein féle módosításokkal nem kell számolnunk.

Egyetemes tömegvonzás törvénye

A világmindenség minden tárgya vonzza egymást; ennek ereje arányos a két test tömegével, és fordítottan arányos távolságuk négyzetével. Minden tárgy tömegével fordítottan arányos mértékben gyorsul az erõ irányába. Testek sebességének, mozgási irányának megváltoztatásához erõ szükséges.

F a gravitációs vonzóerõ, G a gravitációs konstans, cgs rendszerben G = 6,67 x 10^-8 g^-1 cm³ sec^-2. Egy kiterjedéssel rendelkezõ test esetében az r-et a test pontjainak x,y,z koordinátái helyettesítik. Bevezetve az U gravitációs ekvipotenciális felületet, az F erõ az az erõ, amely erre a felszínre merõleges, azaz

Az U konstans (ekvipotenciális felület), és a gravitációs erõ nagysága -dU/dn ahol dU az U változása a dn távolságon belül, az ekvipotenciális felületre merõleges irányban.

A gravitáció szerepe a fizikai földtanban tárgyalt összes jelenség esetében alapvetõ, például:

• termeli a föld hõenergiáját - az árapály erõ okozta súrlódás következtében
• meghatározza a magmás feltörések helyét - a melegpontokon kialakuló sebességkülönbségbõl eredõ felhajtóerõ létrejöttével
• kiváltja a diagenezist - az üledékekre ható fokozódó terhelés - eltemetõdés - kialakulásával
• megszabja a lepusztulás - lehordódás sebességét - a szállitó felszíni vizek helyzeti energiája útján.
• meghatározza a légkör összetételét - könnyebb molekulák (H, He) könnyebben szöknek, mint a nehezebb gázmolekulák (O₂, N₂)

Gravitációs energia

A gravitációs energiát egy test összes pontjában érvényes gravitációs potenciálok összege adja. Azaz, ennyi energia szükséges ahhoz, hogy a tárgy/test minden egyes alkotó tömegrészét az összes egyéb alkotó tömegrész vonzása ellenében a végtelenbe továbbítsa. Ennek fordítottjaként, ez az az energia, amely felszabadul akkor, ha az alkotó tömegrészekbõl, amelyek kezdetben egymáshoz képest a végtelenben voltak, egymás felé esve egy új objektum alakul ki. Egyszerû számitással, egy R sugarú és M tömegû homogén gömbre

Az egységnyi tömegre esõ gravitációs energia E/M uniform Föld esetében 3U/5 lenne, azaz 4 x 10¹¹ ergs/s. Ilyen mértékû energia hirtelen felszabadulása esetében a Föld anyaga elgõzölögne. Ez korlátot szab az akkréciós keletkezés (eszerint a Föld csillagközi porból gravitációs hatásra összetömörödõ égitest) sebességének is, amely így nem lehet nagyobb, mint amennyinél a felszínrõl kisugárzódó hõ termeléséhez elegendõ mennyiségû energia termelõdik.

A Hold Föld körüli pályája

Egy tárgy a Föld felszínén az elsõ másodpercben 4,9 m-t esik a Föld felé. Ha a gravitációs törvény egyetemes, a Holdnak is arányos sebességgel esnie kell a Föld felé. A Hold zuhan, mivel nem érintõ pályán egyenes vonalban halad, hanem körpályán kering. A holdpálya sugara 384 000 km, Föld körüli keringési ideje 29 nap. Ebbõl számítható, hogy a Hold 1 sec alatt 1,36 mm-t esik, azaz kerül közelebb a Földhöz az egyenes vonalú egyenletes mozgáshoz képest. Ez jól illeszkedik a gravitációs törvény által megbecsülhetõ "eséshez".

A Föld sugara 6370 km - ha egy tárgy a Föld középpontjától 6370 km távolságban 1 s alatt 4,9 m-t esik, akkor 384000 km-nyire, azaz 60-szor távolabbról 1/60²azaz 1/3600 x 4,9 m-t zuhan - ez 1,36 mm.

Az esés ellenére azért nem kerül a Hold közelebb a Földhöz, mert a Föld "elkanyarodik" tõle, s így a Föld "körül" esik.

Szökési sebesség

Bármely olyan tárgy, amely a Földtõl v sebességgel, és az U értékénél v²/2-vel nagyobb kinetikus energiával távolodik, nem fog visszaesni, mivel az energia elegendõ ahhoz, hogy a tárgyat hiperbolikus pályán a végtelenbe továbbítsa. Ez a Föld esetében 11 km/sec.

A Föld alakja

Mivel az erõ = tömeg x gyorsulás, ezért azt a vonzóerõt, amelyet a Föld fejt ki egységnyi tömegre, gravitációs gyorsulásnak nevezzük, és g-vel jelöljük. Ennek mértéke 982,7 gal, pontról pontra változik. Tengerszinten a változás kicsi, 0,5 %. A g mindenütt merõleges az U ekvipotenciális felületre. Nyugalomban lévõ folyadék felszínre ható összes erõ a felületre merõleges, különben elmozdulást, áramlást okozna. A tengerszint tehát az a felület, amelyre vonatkozóan az U konstans. Ha a Föld homogén nem-forgó tömeg lenne, akkor az ekvipotenciális felületek gömbök lennének, s ilyen lenne az óceán felszíne is.

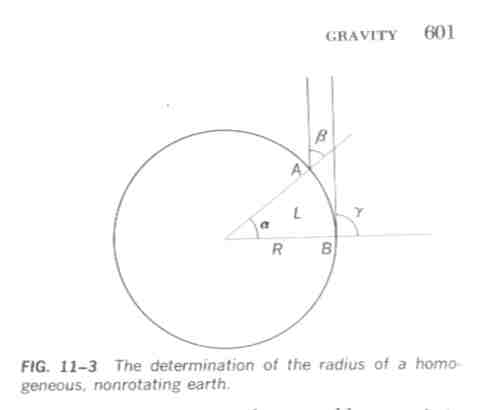
A Föld sugarát ennek ismeretében meghatározhatjuk, ha a Föld középpontja felé mutató vertikálishoz hasonlítva két ponton megmérjük egy Földön kívüli csillagászati pont irányával bezárt szöget. A két ponton mért szögkülönbség azonos a két ponton a Föld középpontja felé bocsátott vertikális által bezár központi szöggel. A központi szög és a hozzátartozó megmérhetõ ívhossz ismeretében meghatározható a Föld sugara. A mérést már Erathostenes (296-196 i.e.) elvégezte.

Mivel a Föld forog, alakja csak közelítõen gömb alakú, valójában forgási ellipszoid. Ennek oka a gravitáció ellenében ható, és a forgásból adódó centrifugális erõ, amely a legkisebb a pólusokon, a legnagyobb az egyenlítõ síkjában. A forgásból származik a lapultság - ennek értéke 1/298,5.

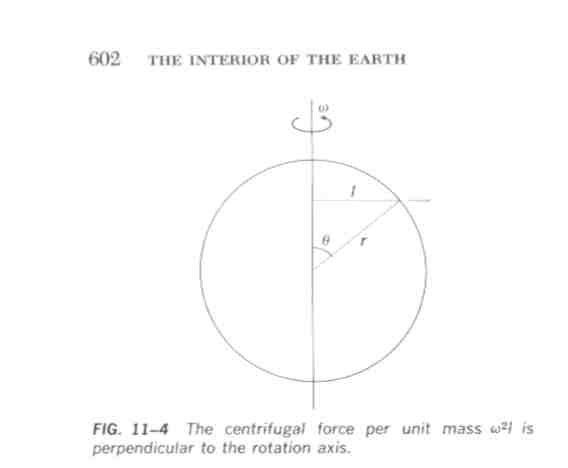
A centrifugális erõ és a gravitációs erõ a Föld minden pontján eltérõ irányú vektor, s csak a pólusokon és az Egyenlítõn esik egybe. Ezért az ekvipotenciális felület (melyre a két vektor eredõje merõleges) ellipszoid, amelynek rövid és hossztengelye a Föld forgástengelyével illetve az Egyenlítõ síkjával esik egybe.

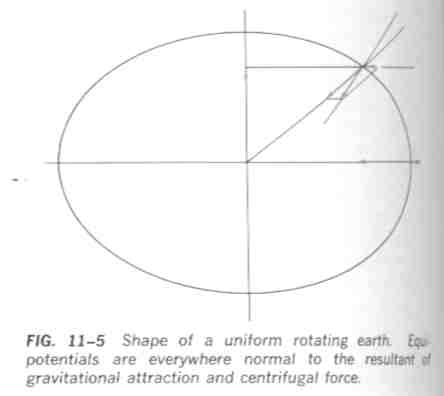
A szferoid az az ekvipotenciális felület, amely az áltagos tengerszinttel megegyezik egy olyan képzeletbeli forgó Földön, amelyen a tömegek felületbeli eloszlása homogén, azaz a hegységek és a tengerek szintkülönbségei ki vannak egyenlítve. A valóság még bonyolultabb, annak következtében, hogy a Föld tömegeloszlásában inhomogenitások vannak. Igy tehát az ellipszoidokkal csak közelíthetjük a valóságos alakot. A valóságos Föld alakhoz tartozó ekvipotenciális felületet nevezzük geoidnak.

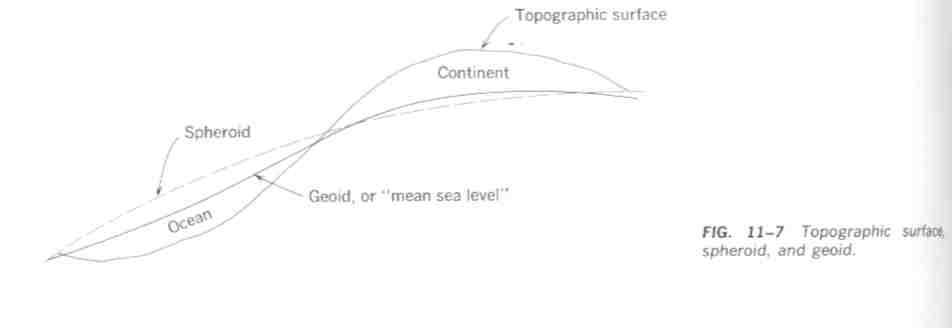
Izosztázia

A 18 században Pierre Bouguer francia fizikus akarta megmérni a Föld egyenlitõi sugarát Peruban. Azt várta, hogy a közeli hegyek tömege arányos mértékben eltéríti a függõónt, de nem így történt. Everest ugyanezt találta Indiában, a Himalája tömeghatását vizsgálva.

Két külön pontban, de azonos szélességen végzett g mérés különbözhet egymástól. Ennek okai lehetnek:

1. A mérések rendszerint nem a szferoidon, hanem magasabban történnek. A Föld középpontjától távolabb a gravitáció csökken. A "szabad-levegõ" korrekciót hozzáadva az alacsonyabb szinti méréshez, kapjuk a szabad-levegõ anomáliát.
2. A szferoidra számitott gravitációnál azt tételezzük fel, hogy a teljes tömeg a szferoidfelület alatt van. A valóságban a szferoid és a topográfiai felszín között tömegek helyezkednek el. Ezek hatását a Bouguer-korrekcióval lehet figyelembe venni.

A szabad levegõ anomáliához hozzáadva a szabad-levegõ korrekciót, és levonva a Bouguer korrekciót, kapjuk a Bouger anomáliát. A meglepõ az, hogy ez az anomália a szárazulaton sokszor negatív, és számszerint nagyobb, mint a szabad levegõ anomália, mintha látszólag a szferoid felület feletti kõzetlemeznek nem lenne tömege.

Ez a jelenség, amely általánosnak tûnik, az izosztázia. Ennek földtani jelentése az, hogy a függõleges kõzetoszlop tömege a Földön mindenütt ugyanakkora, függetlenül a topográfiától és a magasságtól, a kontinenseken és az óceánokon egyaránt. Ha tehát a kõzetoszlop sûrüsége kisebb, akkor térfogata nagyobb (és ezért a felületrõl jobban kiemelkedik).

A jelenség hasonló a hidrosztatikus egyensúlyhoz. Egy nyugalomban levõ folyadékban egyazon felületen, ekvipotenciális felszínen a nyomás ugyanakkora, máskülönben áramlás indulna meg. A folyadék felszín alatti bármely h mélységben a nyomás (azaz az egységnyi felületre ható erõ) egyenlõ a g, illetve az egységnyi keresztmetszeti felületû anyaghasáb tömegének szorzatával.

A kõzetoszlopok tömegének azonosságára a legjobban alkalmazható az Airy modell, amelynél azt feltételezik, hogy egy-egy kõzetoszlopban eltérõ arányban vesznek részt különbözõ sûrûségû anyagok. Tudjuk, hogy a köpeny a Moho alatt nagyobb sûrûségû, mint a kéreg a Moho felett. A tömegek egyenlõsége e modell szerint úgy állna elõ, hogy a kéreg a kiemelkedett területeken vastagabb mint a mély területeken.

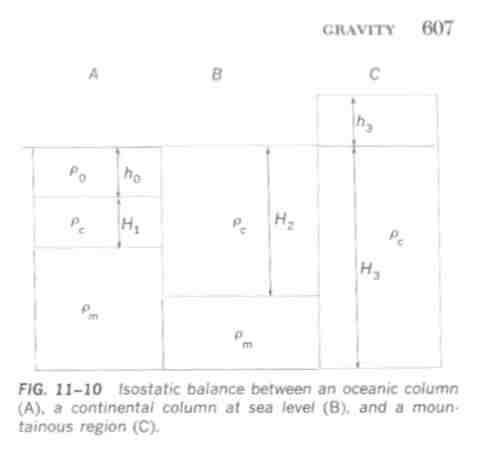
A fenti ábra három különbözõ típusú kéregblokkot mutat be, az A blokk óceáni, a B blokk kontinentális tengerszinti, a C blokk kontinentális magashegységi blokk. A három blokk közül a legmagasabb Moho helyzet az A blokkban, a legmélyebb Moho helyzet a C blokkban feltételezhetõ.

A fenti korreláció helyességét szeizmikus adatok nagy vonalakban igazolták. A legmélyebb Moho helyzeteket eddig a Pamírban és a chilei Andokban mérték, 70 km körüli kéregvastagsággal.

Izosztatikus anomáliák

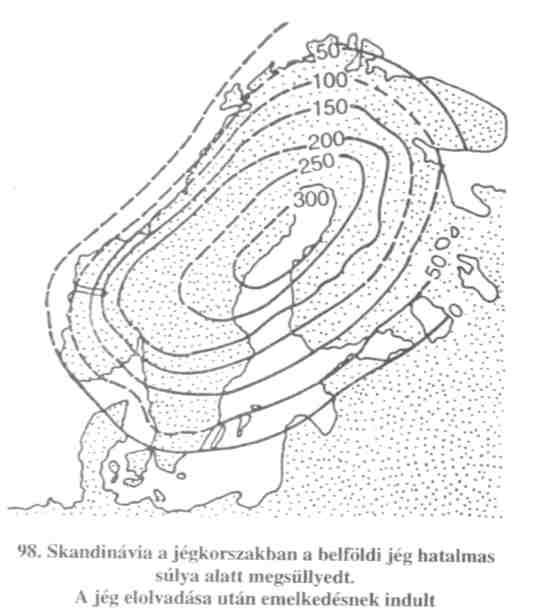
A Föld területének legnagyobb része izosztatikus egyensúlyban van, de vannak anomális területek. Ezek olyan területek, ahol a Bouger-anomáliát sem a kéregvastagság, sem a sûrûség valószínûsíthetõ értékei nem redukálják nullára. Pozitív anomália tömegtöbbletet, negatív anomália tömeghiányt jelent. Pozitív anomália van pl. Hawaiin, ahol a friss lávatömegek alatt a kéreg még nem süllyedt megfelelõ mélységre, további süllyedés várható. Negatív anomália pl. Skandinávia, ahol a terület a szárazulati jégtakaró elolvadása miatt emelkedik. Az alábbi diagram Skandinávia kiemelkedésének mértékét mutatja a jégkorszak óta. Az emelkedés mértéke helyenként még ma is eléri az 1 cm-t.

Gravitációmérések alkalmazása a gyakorlatban

A gravitációs mérések jelentõs szerepet kapnak minden olyan földtani probléma megoldásában, ahol viszonylag jól meghatározható geometriájú alakban, helyzetben jelentõsen eltérõ sûrûségû kõzettömegek kimutatása a cél. Sokféle ilyen feladat lehetséges, vulkáni centrumok kimutatásától kezdõdõen szkarnos érctestek helyzetének meghatározásáig. Jelentõs a módszer alkalmazása a szerkezetföldtani kutatások területén, és szénhidrogén-kutatásokban.

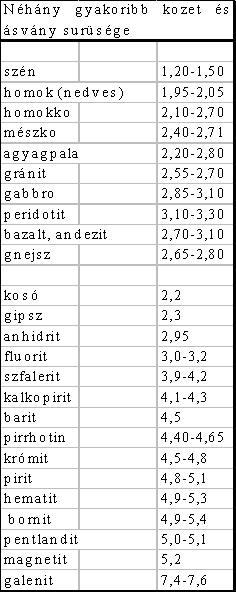
Ugyancsak jelentõs szerepe van a gravitációnak az eljárástechnikában - a kõzetek és ásványok megfelelõ sûrûségkülönbség esetén elválaszthatók a gravitáció - eltérõ süllyedési sebesség - segítségével.